Eine interessante neue Aufgabe:
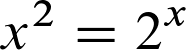
Für welche Zahlenwerte der Variablen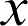 ist die Gleichung korrekt?
ist die Gleichung korrekt?
Hinweis: Es gibt 3 Lösungen für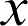 , die diese Bedingung erfüllen.
, die diese Bedingung erfüllen.
Viel Spaß!


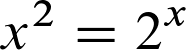
Für welche Zahlenwerte der Variablen
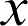 ist die Gleichung korrekt?
ist die Gleichung korrekt?Hinweis: Es gibt 3 Lösungen für
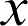 , die diese Bedingung erfüllen.
, die diese Bedingung erfüllen.Viel Spaß!




